PHILIGHT- Mon, 13 Nov 2000

---

All new Pictorial Summary: ../summary (link at sitemap)

Note - in the below: the measured? - 4.32 x C (lightspeed) is = 1.618 ^ 3 x lightspeed, (Golden Mean cubed.. ) The original ../predictions papers predicted that velocities faster than light would specifically be accomplished and measured as multiples of PHI. Which would confirm that the optimization of recursion / embedded geometrically identified with PHI / Golden Ratio, would create the implosion worm adding and multiplying of wave VELOCITIES thru light speed!.. Dan Winter

also related - in the PHI harmonics in DNA animations from ../superDNA (link at sitemap) - Is DNA's superconductant AND superlumenal (faster than light wave propagation - see Pensinger) quality derived from the Phi Harmonics in it's Dodeca braid geometry, and further imploded when those harmonics are embedded into Phi recursion long phonon sound waves by HEART EKG going into Bliss? (Charge Density) - Academic Reference:.D. A. Paine and W. L. Pensinger. "A Dynamical Theory Describing Superconductant DNA." International Journal of Quantum Chemistry, 15:3,
pp. 333-341, 1979. Discussed at http://www.peaknet.org/webpages/autopoy/ithapapers/text.html#DNA

the below courtesy of ANANDA:

http://www.akasha.de/~aton/SuperPHImai l.html

PHI HARMONICS IN FASTER-THAN-LIGHT QUANTUM TUNNELLING

For Dan Winter

By Ananda, ATON Institute, Norway.

Copyright © 2000, by Ananda ® and ATON Vase DA ®, Norway

---

 

(Another updated version of this will follow, with many graphs and pictures)

With the global media's announcement this year of faster-than-light signalling, commencing in the Scientific American September issue's reportage, as well as their announcement of the multidimensional universe, to be tested in 2005, at the CERN particle accelerator in Switzerland, there appears to be a revolution at hand, amidst mainstream discoveries. A revolution that began some 7 years earlier, and that could be set to shake the very foundation of what we call reality, depending on further research.

In this article, we look at the apparent PHI, or golden number harmonics, that are described in some of these superluminal experiments. Their appearence here may yield extreme significance, in a vast array of fields, from charting the universe, it matrix and laws, and beyond, all the way to the personal including biofeedback enhancement in superlearning techniques and whole body intelligence.

However, this research began to receive attention when the following obscure science paper highlighted their first glimpse of superluminality:

 

"Our results were consistent with the group delay predictions, and also with Buttiker's proposed Larmor time, but not with the "semiclassical" time. The measured times exceeded the predictions by approximately 0.5 fs [femto seconds], but this result was at the borderline of statistical significance, and not discussed. Since then, further data taken at various angles of incidence have continued to show a discrepancy, ranging from an excess of 0.5 fs near normal incidence to a decit of over 1 fs at large angles of incidence."

­Sub-femtosecond determination of transmission delay times for a dielectric mirror (photonic bandgap) as a function of angle of incidence. Aephraim M. Steinberg and Raymond Y. Chiao Department of Physics, U.C. Berkeley, Berkeley, CA 94720, Internet: aephraim@physics.berkeley.edu. Quant- ph/ 9501013 16 Jan 95. (Preprint quant-ph/9501013; Received Phys. Rev. 17 August, 1994), page 2

During the mid 1990s the European media highlighted a potential science shattering discovery, faster-than-light signalling of Mozart's 40th Symphony. Our specialised magazine Vortexijah (issue 4/5, Autumn 1994) also reported on this odd finding, which was stated to be a "failure in causality", Einstein's version of Karma, or cause and effect, which states that nothing goes faster than the speed of light.

Amidst this European media spur, was a 1995 article in the conservative foundation stone news paper of Germany, de Zeit, which published this as a headline story entitled: "Mozart's Symphony #40 Causes Breakdown In Modern Physics."

We were given a clipping, without the date, which was approximately June 1995. Here are some excerpts translated into English:

"Koeln physics professor Guenther Nimtz, used a hollow metal pipe, called a wave transducer. On the end of the Ca. 20 cm long metal pipe a section of Mozart's Symphony #40 became audible through an amplifier. Not digital quality, but good enough for radio. There was a speed change of the waves that were transduced. This tunnel effect was 4.7 x C [c = speed of light]. The lengths of the microwaves that Nimtz chose were actually too wide for the wave transducer. But still some of them found their way through the other side to the amplifier. In the tunnel occurrence the waves do not seem to require any time. Whereas outside the tunnel the waves were well behaving enough to follow the classical laws and travel at the speed of light. Mozart's symphony has information content, Nimtz contends."

 

Such an almost unbelievable news item, herein without a date, however was based on actual accepted research. Here I quote Dr. Raymond Chiao's brief summary of these experiments:

"Other experiments confirming the superluminality of tunnelling have been performed in Cologne, Florence, and Vienna [14, 15, 16]. The Cologne and Florence groups performed microwave experiments, and the Vienna group performed a femtosecond laser experiment. All these groups have confirmed the Hartman effect. One of these groups [17] has claimed to have sent Mozart's 40th symphony at a speed of 4:7c through a microwave tunnel barrier 114 mm long consisting of a periodic dielectric structure similar to our dielectric mirror."

--Quantum Nonlocality in Two-Photon Raymond Y. Chiao , Paul G. Kwiat z and Aephraim M. Steinberg. Department of Physics, University of California, Berkeley, CA 94720-7300, December 21, 1994). Pp 10.

We will return to the PHI significance of this above figure a little further ahead.

As I have been speaking about this experiment and others that emerged from other universities, over the years, I mentioned the possibility that we could be enabled to model or understand the 'high dimensions' through which the signal may have transversed, by the Golden Mean or PHI.

I related, over the years, that PHI would be the first localised form of the virtual, and in making cosmological models that are post-infinite maps. Mentioning that PHI would be the best model of coherence, or highest order, that is the simplest pathway by which the nature of this dimension could translate, or mirror in personification, the coherent pathways of those vacuum hyperspaces, even though they may be post-PHI therein. Never-the-less in our localised spatial dimension, PHI would be the simplest constant which would personify the unique signals of these N-spaces. Naturally I was influenced in making such above cosmological speculative models, by basic material on PHI by colleagues.

My colleague Daniel Winter, (who studied with the later Buckminster Fuller, and is an expert on sacred geometry, in the sense of being a public hero in exposing and breaking down into more understandable terms for the layman, many arcane sacred geometrical principles and relationships, which the public at large has never been exposed to before), predicted now, for several years, that faster-than-light signals would be found to travel in the PHI ratios.

His own modelling bore this out. He also has another angle, logic and theory for this, whereby the faster-than-light dimensions are domains of pure fractal implosion, in every direction the greater superluminal harmonics to infinity. This particular article has come into formation, when Dan asked me for references upon my mentioning PHI harmonics in superluminal tunnelling, whilst we were lecturing together in SION, Switzerland, September 2000.

My own modelling herein is perhaps in far more controversial ground, whereby we explore Virtual Field Intergeometries, and Monatomic element's Meisner Field transforms into full superconductive fusion -- a new and very controversial field as of yet (some animated models of intergeometrical monatomic elements at Intergeometry). If such Virtual and monatomic intergeometries were in localised fields, some of these could be considered as quantum decoherence, in their effect, except with the unique attributes of 8 hz phase-conjugation, that Dr. Andrija Puharich discovered in the late 1970s, and patented in his Protocommunication II.

Dr. Chiao, however, does indicate that the superluminal transportation does involve decoherence of the local photons as well:

"The superluminality can be understood by thinking of the low transmission through our barrier as arising from destructive interference between waves which have spent different lengths of time in the barrier. "

--tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998. Pp 10.

Although, in the monatomic intergeometries, any photon group, would be infrared coherent laser, which in increased critical thermal exposures, phase-cancel each other out, this also became apparent in the faster-than-light experiments listed in the September 2000, issue of the Scientific American entitled "Unlimited Light", pp 18:

"The researchers used a combination of laser beams to create an usual region of 'anomalous dispersion' in the six centimeters of cesium gas, where the velocity of light is higher for higher frequencies of light (ordinarily higher frequencies mean lower speeds).

"This region causes the pulse to 're-phase,' according to Wang. The light pulse, all of whose constituent wavelengths overlap constructively, loses its phase alignment as it propagates toward the cell, causing the waves to cancel one another out. "

Hence, what we have modelled with Vortexijah phase-conjugation models, and further intergeometrical explorations, here appear to be an essential part in the superluminal transmission of light, at least on the quantum level. But much more significant confirmations on our Vortexijah models on a more concrete level, have come in, from the American Scientist, in terms of superconduction experiments (which we will report on elsewhere).

This article is not intended to discuss this particle issue of our Intergeometry models any further, and my colleague Dan Winter's models can be found on his web site. I came into writing this piece, in the process of supplying my colleague with the references to the superluminal speeds related to PHI.

This itself is an exciting level of discovery, which is destined to produce a wide array of theories to describe them, classical and mainstream, to the fringe and daring novel visionary science explorations, for those who do not have a position with a mainstream university to compensate exploration and novelty for.

 

SUPERLUMINOSITY YIELDS PHI

Now what of Dr. Nimtz reported signalling of microwaves to come out 4.7 times faster than light tuned in Mozart? This is an interesting figure, considering that the sacred Pythagorean constant PHI, figures into this number. PHI is generally generalised as 1.618 or 0.618. When we add onto of 1.618 five times 0.618 (3.09), the result is 4.7 (4.708 to be precise). Mozart yielded an astounding harmonic sequence, back in 1995.

Other experiments were then enabled which used other devices, and which lead to similar results:

"Experiments have shown that individual photons penetrate an optical tunnel barrier with an effective group velocity considerably greater than the vacuum speed of light. The experiments were conducted with a two-photon parametric down-conversion light source, which produced correlated, but random, emissions of photon pairs. The two photons of a given pair were emitted in slightly different directions so that one photon passed through the tunnel barrier, while the other photon passed through the vacuum. The time delay for the tunnelling photon relative to its twin was measured by adjusting the path length difference between the two photons in a Hong-Ou-Mandel interferometer, in order to achieve coincidence detection. We found that the photon transit time through the barrier was smaller than the twin photon's transit time through an equal distance in vacuum, indicating that the process of tunnelling in quantum mechanics is superluminal. Various conflicting theories of tunnelling times are compared with experiment."

"tunnelling, the quantum mechanical process by which a particle can penetrate a classically forbidden region of space, is one of the most mysterious phenomena of quantum mechanics. Yet it is one of the most basic and important processes in Nature, without which we could not even exist, for tunnelling is involved in the very rst step of the nuclear reaction, p +p ! d +e +e, which powers the Sun, the source of energy for life on the Earth."

--Tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998

In the above cited research, the result was an objective measurement of the superluminal tunnelling speed, and which has a near PHI value, which here is probably too far off pure PHI to be noticed, but in others PHI perfects, it is not discussed either by the researchers:

"After traversing the tunnel barrier, the peak of a photon wave packet arrived 1:47 ±0:21 fs earlier than it would had it traversed only vacuum."

--tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998. Pp 10.

 

Naturally add 1:47 and 0:21 and there we have a proximity to PHI with 1.68, as compared to 1.618, and apart from numerous PHI perfects and relatives, there are numerous proximity's to PHI as well, just as the EKG work of colleague Daniel Winter has slight variants in the magnetic signature harmonics from the heart cardio beat at moments of coherence.

Other almost perfect results that are at PHI, which were first predicted and then confirmed are mentioned in the following:

 

The Wigner theory predicted at midgap a tunnelling delay time of around 2 fs, or an effective tunnelling velocity of 1:8 c. The Buttiker-Landauer theory predicted at midgap an infinite effective tunnelling velocity, which implies a zero tunnelling time.

--tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998. Pp 8.

 

Of course the infinite velocity is of exceptional interest, I personally had been predicting this since 1993, and my colleague Daniel Winter has likewise, but from another, yet more than complementary, angle.

But what is of significance in these predictions, and their confirmation, which is to follow, is the 1:8 x faster-than-light tunnelling velocity. This is an almost perfect 3 x PHI 0.618 which equals 1.854, which here is a margin of error so slight that this is a clear Golden PHI hit. But from theory to practice, here these figures are confirmed:

 

"Recently, an experiment indicating the simultaneous existence of two different tunnelling times was performed in Rennes [18]. In frustrated total refl ection (FTIR), the tunnelling of photons through an air gap occurs between two glass prisms when a light beam is incident upon this gap beyond the critical angle. The Rennes group observed in FTIR both a lateral displacement of the tunnelling beam of light and an angular de flection of this beam. These two effects could be interpreted as evidence for two different tunnelling times that simultaneously occurred in the same tunnelling barrier. The lateral displacement is related to the Wigner time, and the angular detection is related to the Buttiker-Landauer time. As evidence for this, they cited the saturation of the beam displacement (the Hartman effect), and the linear increase of the beam detection, as the gap was increased."

--tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998. Pp 11.

 

Hence, the PHI approximate Wigner time velocity tunnelling of 1:8 faster-than-light is an actuality, further confirming our and others predictions. We should also remember that PHI harmonics are in the DNA double helix proportions themselves: height 34 angstroms and width 21 angstroms (these are rounded of PHI numbers and follow the Fibonacci sequence of numbers, which as they progress into higher orders, come ever closer to the perfect PHI. For instance the number 144 in the Fibonacci sequence is also 89 times PHI 1.618 = 144.002 (89 is also the preceding Fibonacci number before 144 from the addition 89 + 55).

This, however, is just the beginning, of the objectification of some very exciting new theories, which also validates the essentiality of novel modelling of the the Virtual domains through which the superluminal tunnelling is passing, in a series of octaves, which are PHI related and infinite, modelling by both PHI fractal platonic solid and PHI spiral asymmetrical interelationships (as my colleague Daniel Winter has avidly dedicated a good portion of his life to fulfilling), and intergeomtrical models, which sequence the superluminal intergeometrical versions of the Platonic solids, through all inter-relationship phase-conjugate spins, in the post-polarity domains of the faster-than-light realms, where the poles of cause and effect have interpenetrated through each other.

This also leads to the unveiling of yet another mystery, which some novel colleagues already have made ardent strides to graph and map its illusive fractality (i.e.Sheliac, Los Alamos Labs), and PHI spiral modelling of time:

 

"It is now clear that one cannot rule out the Wigner time simply on the grounds that it yields a superluminal tunnelling time. It also appears that there may exist more than one tunnelling time. Hopefully, the mysterious role of time in quantum mechanics will be elucidated by these studies."

--tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998. Pp 12.

 

Since 1998 there have been further tunnelling experiments, and it is these that have seen recent public media highlighting. There is more than one tunnelling time harmonic. And certainly quantum time is taking a new stand in terms of mode lability. The shadow of this understanding, as Sheliac has demonstrated in temporal experiments at Los Alamos National Laboratories, upon analysing time in the nucleus of the atom, is one common element: fractality. Coherent fractality is evidenced in our universe by both the Fibonacci series of numbers, and its perfected partner the PHI harmonic cascade, where the scale changes, but the ratio remains the same, and no information is lost, mirror-to-mirror.

PHI is the only constant which can be divided by itself, to yield itself, and be multiplied by itself to yield itself, as occurs in the perfect hyterodyning of toroidal waveforms. In other words when two coherent wave toroids make love, their children [hyterdyning], are the sum of the two parental toroids multiplication and addition of themselves and each other, this renders the wavelength of their children).

Now in the new research, the May 30, 2000 issue of the New York Times publishes an article by James Glanz, entitled "Physics Approaching Speed of Light Mind-bending new studies appear to break Einstein's rules", and reports:

"In the most striking of the new experiments, a pulse of light that passes through a transparent chamber filled with specially prepared cesium gas appears to be pushed to speeds of 300 times the normal speed of light. That is so fast that, under these peculiar circumstances, the main part of the pulse exits the chamber even before it enters. "

This article was written whilst I was trying to retrace one experiment that mentioned superluminal speeds of 4.3 or 4.32 (which at present I have not been able to retrieve, but suspect it is on the German 1998 television documentary on Dr. Chiao's work, which I am in the process of obtaining again from the source that gave me the initial copy.

Why was the 4.32 so important. Actually any decimal harmonic of it, like 432 or 43,200 is of value. For this is another approach to PHI. We look here at the figures in geometry. The platonic solid the dodecahedron, is a perfect symmetrical object that can beautifully map PHI, and a dodecahdron can be constructed by 5 cubes. With the first cube tilted at -64 on its X axis, the next cube is tilted at 72° on the Y-axis, followed by 144; 216; and 288. Hence, 5 cubes at 72° on the Y-axis.

What has 72° to do with PHI? A golden mean triangle is made by taking one horizontal line, any length, as base, and then extending two 72° lines vertically up until they kiss each other. Five of these golden triangles, with each respective base tilted at 36° renders the Pythagorean pentagramme within a pentagon, the perfect persona for PHI. 5 cubes at 72°; 5 golden triangles at 72°. The first a 3D object of 12 pentagon faces, the latter a 2D single face.

6 x 72 renders 432. When a dodecahedron's 12 pentagon faces are used to map number sequence degree's, then some astounding numbers emerge from this 3D PHI complex. Taking the first pentagon, it is comprised of 5 36° lines. Hence, 36; 72, 108; 144; 180. The next face then continues this sequence: 216; 252; 288; 324; 360, and so forth, now continuing on the next neighbouring face: 396; 432...

Hence, we now have travelled on a geometrical visual journey to discover the 432 connection to PHI, any decimal harmonic of this number can be utilised to construct the same geometrical PHI complex. Take for instance 43,200, the number of seconds in 12 hours, this is 600 times 72°. Hence, make a complex of 20 dodecahedrons.

This can be done simply by stellating each of the 12 pentagon faces with 5-sided pyramids, and their capstones enable the construction of the 20 icosahedron triangular faces (another PHI complex, and this cascade from dodecahedron to icosahedron is a golden one). Then stellating each of the 20 triangular faces with the platonic solid called the tetrahedron (a pyramid of 3 triangular faces one a fourth base triangle), and their tips, or capstones make the vertices for the 12 pentagons of the dodecahedron (if one needs a little aid in visualising, there are some animated basic models at Intergeometry which should aid one on the way to this).

Do this another 18 times, and one has a stellation PHI complex of 20 dodecahedrons. On each dodecahedron the number sequence continues. I.e. from 2,160 of the first dodeca, we commence to the next stellated dodeca: 2,196; 2,232; 2,268; 2,304; 2,340 etc. With the last pentagon point of dodecahedron 20 giving 43,200°. One could also do this with dodecahedrons of the same scale, making a daisy chain from the north and south face, of 20 dodecahedrons, linked by their faces, and the last 36° point of the 20th dodecahedron is 43,200° from the initial first 36° base of the first dodecahedron.

A PHI complex arcade and cascade of fractality. But what has this to do with the 300 times faster than light speed? Captain Bruce Cathie brought to light some significant equations to the public at large, in a series of books spanning some 40 years of mathematical research.

Amidst this, he pointed out that the vacuum speed of light, when measured in nautical mile grid seconds, a universal measure that can be used throughout the galaxy and universe, not limited to a single planet in its measure, then converting the standard measure of the speed of light from miles per second to nautical mile grid units, the translation is precisely 144,000 nautical mile grid seconds.

300 times 144,000 renders 43,200,000 -- a perfect decimal harmonic of 43,200, which can be comprised of 20,000 stellated dodecahedrons in PHI. If this figure reported by the New York Times, the San Francisco Chronicle, and the Times News Network is correct, then we have an enormous new PHI view on the superluminal fractality universe of implosion, or the imploverse.

OVERVIEW: 300 TIMES 144,000 MINUTES OF ARC PER EARTH GRID SECOND IN A VACUUM FOR THE SPEED OF LIGHT = 43,200,000, this decimal harmonic of 432 and 24 hours in second 43,200, and the Great Pyramids polar radius ratio to Earth from the multiplication of its original height by 43,200, as well as its base (in multiplication of 43,200) to the circumference of the equator, may be quite interesting. Geometrically these decimal harmonics are extremely interesting.

Before we continue looking at other PHI harmonics within the scientific literature, let us look at an alternative perspective for the same. In the November 1998 paper prepared for the science journal Nature, Dr's M. A Nielsen, E. Knill, and R. Laflamme, entitled: "Complete Teleportation":

"One of the most unexpected is a procedure called quantum teleportation that allows the quantum state of a system to be transported from one location to another, without moving through intervening space. Partial implementations of teleportation over macroscopic distances have been achieved using optical systems, but omit the final stage of the teleportation procedure. Here we report an experimental implementation of the full quantum teleportation over inter-atomic distances, using liquid state nuclear magnetic resonance (NMR). The inclusion of the final stage enables for the first time a teleportation implementation which may be used as a subroutine in larger quantum computations, or for quantum communication. Our experiment also demonstrates the use of quantum process tomography, a procedure to completely characterise the dynamics of a quantum system. Finally, we demonstrate a controlled exploitation of decoherence as a tool to assist in the performance experiment."

--Complete Teleportation, presented to: Theoretical Astrophysics T-6, MS B-288, Los Alamos National Laboratory, Los Alamos, NM 87545; Department of Physics and Astronomy, University of New Mexico, Albuquerue, NM 87131-1131; Computer Research and Applications CIC-3, MS B265, Los Alamos National Laboratory. October 29, 1998.

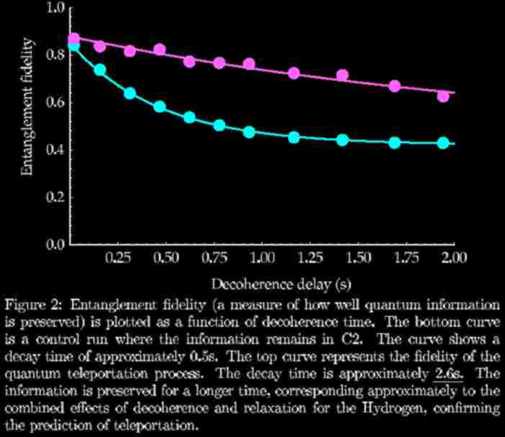
Apart from the outstanding stride over and way beyond the other superluminal experiments, in terms of practicality, whilst knowing that this research was sponsored by "the National Security Agency and the Office of Navel Intelligence for support" (pp 8), the decay time figure for their quantum teleportation process is listed as 2.6 s (femto seconds), as listed in the above graph. 2 femto seconds is equal to 1:8 times the speed of light. Hence, this is 2.25 times C. (1.618 + 0.618 = 2.236, which is very near, but yet off).

Where the significance comes out, however, is when we multiply the vacuum speed of light of 144,000 nautical miles per grid second by 2.25. The geomatria figure that results works perfectly in the geometrical 3D modelling of the PHI complex. For the resulting 324,000, is 9,000 times that 36° for the pentagon lines, and 324,000 in this mapping of degree's fits precisely 150 dodecahedron's, wheather in a PHI cascaded stellation relationship with the icosahedron, or by daisy chaining relationships of their pentagon faces.

Now in extension and conclusion to this present edition of this article (which will be expanded) the Sunday Times and the Times News Network published a story in their respective papers this Summer, as follows:

 

"Dr Raymond Chiao, professor of physics at the University of California at Berkeley, who is familiar with Wang's work, said he was impressed by the findings. 'This is a fascinating experiment,' he said.

"In Italy, another group of physicists has also succeeded in breaking the light speed barrier. In a newly published paper, physicists at the Italian National Research Council described how they propagated microwaves at 25% above normal light speed. The group speculates that it could be possible to transmit information faster than light.

"Dr Guenter Nimtz, of Cologne University, an expert in the field, agrees. He believes that information can be sent faster than light and last week gave a paper describing how it could be done to a conference in Edinburgh."

Indeed, professor Nimtz had succeeded in sending the information that was Mozart's 40th Symphony superluminally, which is not speculation. The 25% mentioned above, if the correct figure, is once again of significance. For 25% of 144,000 nautical miles per grid second, is 36,000 nautical miles per grid second. This is also a 36° pentagon decimal.

Hence, the 25% tunnelling speed exceeding the speed of c, renders 180,000 nautical miles per grid second, in the vacuum. Here we have a decimal harmonic of 180, which is the five 36° lines of the pentagon. It is also 2,500 x 72°, the golden triangle. Hence, another geometrical PHI complex.

 

SUMMARY

We have seen that the microwave tunnelling done by Dr. Nimtz was 4.7 x C, which is a perfect PHI harmonic of 1.618 plus 5 x 0.618.

1. The Wigner theory predicted and was confirmed, that at the midgap there was a tunnelling delay time of around 2 fs, a tunnelling velocity of 1:8 c. An almost perfect 3 x PHI 0.618 which equals 1.854, a so slight error that it remains a PHI hit.
2. Then this summers global media exposures of superluminal tunnelling at 300 x c. 300 x 144,000 nautical miles per grid second (the speed of light) = 43,200,000, a decimal harmonic of 432 and 43,200, which comprises 20,000 dodecahedrons, which each have 2,160° (like the Moons diameter or one Zodical house of precession), which itself is 30 x 72. And the golden triangle is two ascending lines of 72° from the base. 5 of these with their bases at 36° to their neighbours, renders a pentagramme in a pentagon, like 5 cubes tilted 72° on the Y-axis, from the initial cubes -64°, renders a dodecahedron, which has 12 pentagon faces, with pentagrammes visible at the poles. Hence, the dodecahedron is the onederful PHI complex tool for measuring and translating the superluminal PHI relationships.
3. Then we followed with the Quantum teleportation figures of 2.25 x c, or 144,000 x 2.25 = 324,000, which is 9,000 x 36°, and fits a PHI cascaded PHI-complex of 150 dodecahedrons.
4. Lastly there were the microwave experiments from Italy, where microwaves were propagated at 25% x c. 25% of 144,000 = 36,000, yielding 180,000 nautical miles per grid second, which fits 1,250 pentagon faces, since 180,000 is comprised of 5,000 of those 36° pentagon lines, that make one pentagon face of 5 x 36 = 180°, and it is 2,500 x 72°, the PHI triangle complexion herein is very evident.

 

Whilst the 4.32 figure still needs verification, when we receive the video, it is a more difficult logic to shape this with PHI, but should it turn out to be 4.3 x c, or 4.3 x 144,000 the result is 619,200 nautical miles per grid second, which is in close proximity to 618. In the early research, tunnelling between 0.5 and 2 femto seconds were evident. The 2 femto seconds have been explored as 1:8 x c. One would also want to find all of the figures that were obtained between 0.5 and 2 femto seconds, to see if the 0.618 and the 1.618 were evident therein, that would be a view from another angle again. Some of the above may be significant, especially the Dr. Nimtz 4.7 x c. This is just the beginning.

--Ananda, November 13, 2000

 

EXCERPTS, NOTES, DETAILS, AND REFERENCES:

 

our experiments at Berkeley: the Franson experiment [2,3], the \quantum eraser" [4], the \dispersion-cancellation"

eect [5], and tunnelling-time measurements [6,7]. Let us begin by stating that we consider the EPR phenomenon to

be an \eect," not a \paradox": EPR's experimental predictions are internally consistent, and a contradiction is only

reached if one assumes both EPR's notion of locality and the completeness of quantum mechanics (QM). The three

central elements that constitute the EPR argument are 1) a belief in some of the quantum-mechanical predictions

concerning two separated particles, 2) a very reasonable denition of an \element of reality" [namely, that \if, without

in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a

physical quantity, then there exists an element of physical reality corresponding to this physical quantity"], and 3)

a belief that nature is local, i.e., that no expectation values at a spacetime point x2 can depend on an event at a

spacelike-separated point x1 (this denition of locality is now seen to be more stringent than Einsteinian causality, and

is inconsistent with QM).

--Quantum Nonlocality in Two-Photon Raymond Y. Chiao y , Paul G. Kwiat z and Aephraim M. Steinberg x y Department of Physics, University of California, Berkeley, CA 94720-7300, U.S.A. Institut fur Experimental physik, Universit· at Innsbruck, Technikerstrasse 25, A-6020 Innsbruck, Austria. National Institute of Standards and Technology, Phys A167, Gaithersburg, MD 20899, U.S.A. (Preprint quant-ph/9501016; This version was produced on December 21, 1994). Pp 1

 

Erwin Schr· odinger [14], in response to the EPR paper, pointed out that at the heart of these nonlocal eects is

what he called \entangled states" in quantum mechanics, i.e., nonfactorizable superpositions of product states. For if a two-particle wavefunction were factorizable,

(x1; x2) ="(x1)"(x2) (2)

then the probability of joint detection would also factorize,

j (x1; x2) j

2 = j "(x1) j

2

j "(x2) j

2 (3)

so that the outcomes of two spatially separated measurements would be independent of one another. In cases where the

two-particle state cannot be factorized as above, this means that the quantum-mechanical prediction implies nonlocal

correlations in the behavior of remote particles. The Bohm singlet state (1) is such an entangled state. It predicts

correlations between spin measurements made on the two particles. But these correlations persist even if the particles

and their analyzers are separated by space-like intervals, implying the existence of non-local in uences. Though each

particle considered individually is unpolarized, the two particles will always have opposite spin projections when

measured along the same quantization axis. Einstein et al. would conclude that each spin component is an \element

of reality" in that it would be possible to predict its value with 100% certainty without disturbing the particle, simply

by measuring the corresponding spin component of the particle's twin (a measurement which according to EPR's

locality hypothesis cannot disturb the particle in question). As discussed above, this reasoning led EPR to conclude

that quantum mechanics was incomplete; if one instead considers QM to be a complete theory, one must then admit

the existence of nonlocal eects. As we shall see below, experiment supports this latter interpretation.

--Opt Sit. Pp 2.

 

Using a \fair-sampling" assumption and the

symmetry properties of the interferometer (in particular, that the coincidence rate of the unused ports in Fig. 7

is equal to that of the used ports, an assumption supported by tests done with a third detector not shown in the

gure), we can directly obtain the value of the Bell-parameter S from the coincidence rates obtained at two values

each of °1 and °2. S is a measure of the strength of the correlations between the two particles, evaluated for the

four combinations of the two values of °1 and °2, and according to the Clauser-Horne-Shimony-Holt form of Bell's

inequality [18], satisfy j S j 2 for any local realistic model. For appropriate choices of °1 (45 and 135) and°2 (0

and 90), we obtain S = 2:63 0:08, clearly displaying quantum nonlocality.

--Opt Sit. Pp 5

 

We know that the peak of a classical electromagnetic wavepacket

propagating through a piece of glass will travel at the group velocity, but it is not entirely clear that one can interpret

this classical wavepacket as if it were the wavefunction of the single photon and then use the Born interpretation for

this wavefunction. If this interpretation were correct, then the photon would simply travel at the group velocity in

this medium. However, as Sommerfeld and Brillouin have pointed out [30], at the classical level there are at least ve

kinds of propagation velocities in a dispersive medium: the phase, group, energy, \signal," and front velocities, all of

which dier from one another in the vicinity of an absorption line, where there is a region of anomalous dispersion. In

particular, the group velocity can become \superluminal," i.e., faster than the vacuum speed of light, in these regions.

If the photon were to travel at the group velocity in this medium, would it also travel \superluminally"? If not, then

at which of these velocities does the photon travel in dispersive media? (These questions become especially acute in

media with inverted populations, where o-resonance wavepackets can travel superluminally without attenuation and

with little dispersion [31]; see also the accompanying article by Chiao et al.)

Motivated by the above questions, we did the following experiment. We removed the HWP and the polarizers from

the quantum eraser setup and inserted a piece of glass in the path of one of the photons; see Fig. 17. The glass

slows down the photon which traverses it, and in order to observe the coincidence dip, it is necessary to introduce an

equal, compensating delay " by adjusting the trombone prism. We measured the magnitude of this delay for various

samples of glass and were able to determine traversal times on the order of 35 ps, with 1 fs accuracy. In this way,

we were able to conrm that single photons travel through glass at the group velocity in transparent spectral regions,

an interesting example of particle-wave unity.

Clearly, the interest of measuring optical delays is greatest for media with dispersion. Consider the limiting time-

resolution of this interferometer. For a short wavepacket or pulse, a broad spectrum is necessary. In dispersive media,

however, the broad spectrum required for an ultrafast pulse (or single-photon wavepacket) can lead to a great deal

of dispersion. One might expect that this broadening of the wavepacket would also broaden the coincidence dip in

the HOM interferometer, since the physical explanation of the dip (in terms of which-path information carried by the

photons' arrival times) seems to imply that the width of the dip should be the size of the wavepackets which impinge

on the beam splitter. Thus the tradeo between pulse width and dispersive broadening would place an ultimate

limit on the resolution of a measurement made on a given sample. For example, a 15 fs wavepacket propagating

through half an inch of SF11 glass (one of the samples we studied) would classically broaden to about 60 fs due to

the dispersion in this glass. The nature of the broadening is that of a chirp, i.e., the local frequency sweeps from low

to high values (for normal dispersion, in which redder wavelengths travel faster than bluer wavelengths). Hence the

earlier part of the broadened pulse consists of redder wavelengths, and the later part of this pulse consists of bluer

----opt cit pp 9

 

wavelengths; see Fig. 18.

In our experiment, however, we found that the combination of the time-correlations and energy-correlations exhib-

ited by our entangled photons led to a cancellation of these dispersive eects. While the individual wavepacket which

travels through the glass does broaden according to classical optics, it is impossible to know whether this photon was

re ected or transmitted at the beam splitter (recall Fig. 12). This means that when an individual photon arrives

at a detector, it is unknowable whether it travelled through the glass or whether its conjugate (with anticorrelated

frequency) did so; due to the chirp, the delay in these two cases is opposite, relative to the peak of the wavepacket.

An exact cancellation occurs for the (greatly dominant) linear group-velocity dispersion term, and no appreciable

broadening of the 15 fs interference dip occurs. This is a direct consequence of the nature of the EPR state, in that

it relies on the simultaneous correlations of energy and time. A detailed theoretical analysis predicted these results,

in agreement with the simple argument presented here Coincidence rate (sec -1 )

Coincidence rate (sec -1 )

--- Opt Sir pp 10

 

tunnelling is one of the most striking consequences of quantum mechanics. The Josephson eect in solid state

physics, fusion in nuclear physics, and instantons in high energy physics are all manifestations of this phenomenon.

Every quantum mechanics text treats the calculation of the tunnelling probability. And yet, the issue of how much

time it takes a particle to tunnel through a barrier, a problem rst addressed in the 1930s, remains controversial to

the present day. The question arises because the momentum in the barrier region is imaginary. The rst answer, the

group delay (also known as the \phase time" because it describes the time of appearance of a wavepacket peak by

using the stationary phase approximation), can in certain limits be paradoxically small, implying barrier traversal at

a speed greater than that of light in vacuum [33,34]. This apparent violation of Einstein causality does not arise from

the use of the nonrelativistic Schr· odinger equation, since it also arises in solutions of Maxwell's equations, which are

fully relativistic. It has generally been assumed that such superluminal velocities cannot be physical [30], but in the

case of tunnelling, no resolution has been universally accepted.

As a result of developments in solid state physics, such as tunnelling in heterostructure devices, the issue has

acquired a new sense of urgency since the 1980s, leading to much con icting theoretical work [35{37]. Several

experimental papers presenting more or less indirect measurements of barrier traversal times have appeared. Some

seem to agree with the \semiclassical time" of B· uttiker and Landauer [35,38], while others [39,40] seem to agree with

the group delay (\phase time"). We presented the rst direct time measurement conrming that the time delay in

tunnelling can be superluminal, studying single photons traversing a dielectric mirror [6]. Since then, several microwave

experiments have conrmed that the eective group velocity of classical evanescent waves in various congurations

may be superluminal [41{43]. Also, recently a femtosecond laser experiment has conrmed our earlier ndings of

superluminal tunnelling in dielectric mirrors [44], using classical pulses.

As a result of developments in solid state physics, such as tunnelling in heterostructure devices, the issue has

acquired a new sense of urgency since the 1980s, leading to much con icting theoretical work [35{37]. Several

experimental papers presenting more or less indirect measurements of barrier traversal times have appeared. Some

seem to agree with the \semiclassical time" of B· uttiker and Landauer [35,38], while others [39,40] seem to agree with

the group delay (\phase time"). We presented the rst direct time measurement conrming that the time delay in

tunnelling can be superluminal, studying single photons traversing a dielectric mirror [6]. Since then, several microwave

experiments have conrmed that the eective group velocity of classical evanescent waves in various congurations

may be superluminal [41{43]. Also, recently a femtosecond laser experiment has conrmed our earlier ndings of

superluminal tunnelling in dielectric mirrors [44], using classical pulses.

Our experiment again employs the down-conversion source in a HOM interferometer arrangement. The advantage

of using these conjugate particles is that after one particle traverses a tunnel barrier its time of arrival can be compared

with that of its twin (which encounters no barrier), thus oering a clear operational denition and direct measurement

of the time delay in tunnelling. Since this technique relies on coincidence detection, the particle aspect of tunnelling

can be clearly observed: Each coincidence detection corresponds to a single tunnelling event.

In our apparatus, the tunnel barrier is a multilayer dielectric mirror. Such mirrors are composed of quarter-wave

layers of alternating high- and low-index materials, and hence possess a one-dimensional \photonic band gap" [45],

i.e., a range of frequencies which correspond to pure imaginary values of the wavevector. They are optical realizations

of the Kronig-Penney model of solid state physics, and thus analogous to crystalline solids possessing band gaps, as

well as to superlattices. Our mirrors have an (HL) 5 H structure, where H represents titanium oxide (with an index

of 2.22) and L represents fused silica (with an index of 1.41). Their total thickness d is 1.1 m, implying a traversal

time of d=c = 3:6 fs if a particle were to travel at c. Their band gaps extend approximately from 600 to 800 nm, and

their transmission amplitudes reach a minimum of 1% at 692 nm.

Transmission prob. (%)

Time (fs)

 

The semiclassical time is calculated from the group velocity which would hold inside an innite periodic medium

(i.e., neglecting re ections at the extremities of the barrier). As the wavevector becomes pure imaginary for frequencies

---Opt Cit PP 11

 

within the band gap, so does the semiclassical time; in order to extend it into the band-gap region, we simply drop

the factor of i, in analogy with the interaction time of B· uttiker and Landauer [35]. The \Larmor time" is a measure

of the amount of Larmor precession a tunnelling electron would experience in an innitesimal magnetic eld conned

to the barrier region. B· uttiker has suggested a Larmor time which takes into account the tendency of the transmitted

electrons to align their spins along the magnetic eld as well as the precession about the eld [46]. The group delay

is the derivative of the barrier's transmission phase with respect to the angular frequency of the light, according to

the method of stationary phase. All three times dip below d=c = 3:6 fs and are thus superluminal, although their

detailed behaviors are quite dierent; see Fig. 20. For example, the group delay remains relatively constant near 1.7 fs

over most of the band gap. The semiclassical time, on the other hand, dips below 3.6 fs only over a narrower range

of frequencies, and actually reaches zero at the center of the gap. B· uttiker's Larmor time approaches the group delay

far from the band gap as well as at its center, but diers from it at intermediate points.

 

Our apparatus is shown in Fig. 21. As before, a KDP crystal is pumped by a cw uv laser at 351 nm, producing pairs

of down-conversion photons, directed by mirrors to impinge simultaneously on the surface of a 50/50 beam splitter.

One photon of each pair travels through air, while the conjugate photon impinges on our sample, consisting of an

etalon substrate of fused silica, which is coated over half of one face with the 1.1 m coating described above, and

uncoated on the other half of that face. (The entire opposite face is antire ection coated.) This sample is mounted

on two stacked stages. The rst is a precision translation stage, which can place the sample in either of two positions

transverse to the beam path. In one of these positions, the photon must tunnel through the 1.1 m coating in order

to be transmitted, while in the other position, it travels through 1.1 m of air. In both positions, it traverses the same

thickness of substrate. The second stage allows the sample to be tilted with respect to normal incidence.

If the two photons' wavepackets are made to overlap in time at the beam splitter, the destructive interference

eect described above leads to a theoretical null in the coincidence detection rate. Thus as the path-length dierence

is changed by translating a \trombone" prism with a Burleigh Inchworm system (see Fig. 21) the coincidence rate

exhibits a dip with an rms width of approximately 20 fs, which is the correlation time of the two photons (determined

by their 6 nm bandwidths) [24,32,47]. As explained above, the rate reaches a minimum when the two wavepackets

overlap perfectly at the beam splitter. For this reason, if an extra delay is inserted in one arm of this interferometer

(i.e., by sliding the 1.1m coating into the beam), the prism will need to be translated in order to compensate for

this delay and restore the coincidence minimum. In order to eliminate so far as possible any systematic errors, we

conducted each of our data runs by slowly scanning the prism across the dip, while sliding the coating in and out of

the beam periodically, so that at each prism position we had directly comparable data with and without the barrier.

--Opt Cit Pp 12

 

We found that inserting the barrier at normal incidence (for which it was designed) did in fact cause the dip to be

shifted to a position in which the prism was located farther from the barrier. This determines the sign of the eect:

The external delay had to be lengthened, implying that the mean delay time experienced by the photon inside the

barrier was less than the delay time for propagating through the same distance in air. As we rotated the mirror about

the vertical axis, the bandgap shifted to lower wavelengths according to Bragg's law, and for the p-polarized photons

we studied, the width of the bandgap also diminished due to the decreased re ectivity of the dielectric interfaces at

non-normal incidence (cf. Brewster's angle). Thus at 0, our 702 nm photons are near the center of the bandgap,

while at 55, they are near the band edge, where the transmission is over 40%. As can be seen clearly from Fig. 22, the

delay time changes from a superluminal value to a subluminal one as the angle of incidence is scanned, in agreement

with theory.

 

Our normal-incidence data [6] demonstrated that the semiclassical time was inadequate for describing these prop-

---Opt cit Pp 13

 

We have thus conrmed that the peak of a tunnelling wave packet may indeed far side of a barrier

sooner than if it had been travelling at the vacuum speed of light. No signal can be sent with these smooth wavepackets,

however; only a small portion of the leading edge of the incident Gaussian is actually transmitted, and whether the

photon \collapses" into this portion or into the re ected portion is not under experimental control.

 

The superluminality can be understood by thinking of the low transmission

through our barrier as arising from destructive interference between waves which have spent dierent lengths of time

in the barrier. While the incident wavepacket is rising, multiple re ections can be neglected, since their intensities are

small relative to the partial wave which makes a single pass; thus the destructive interference is not very eective. At

later times, when the elds stored in the barrier have had time to reach a steady state, the interference reduces the

transmission to its steady-state value. Thus the leading edge of the packet is transmitted preferentially with respect

to the rest of the packet, shifting the transmitted peak earlier in time.

 

Recent work based on \weak measurement" theory [48] and the idea of conditional probability distributions for the

position of a quantum particle suggests that this superluminal eect is related to the fact that a tunnelling particle

spends very little time in the barrier region, except within an evanescent decay length of the two barrier edges [49{51].

It is as though the particle \skipped" the bulk of the barrier. Furthermore, the nonlocality is underscored by the fact

that this approach allows one to describe conditional probability distributions for a particle which is rst prepared

incident on the left and later detected emerging on the right. These probability distributions describe in-principle

measurable eects, and do indeed traverse the barrier faster than the vacuum speed of light. They suggest that a

single tunnelling particle could aect the expectation values of two dierent measuring devices located at spacelike

separated positions, so long as the coupling to the devices was too weak to disturb the tunnelling process, and hence

too weak to shift either measuring device by an amount comparable to its intrinsic uncertainty.

--Opt cit Pp 14

 

The experiments which we have described in this paper demonstrate some of the stranger nonlocal features of

quantum mechanics. The rst three of these experiments explore them in connection with the Einstein-Podolsky-

Rosen eect. In the Franson experiment, the behaviors of the two space-like separated particles at the nal beam

splitters (i.e., which exit port they choose) are correlated or anticorrelated with each other, depending on the settings

of the phase shifters in the interferometer. Likewise, in the quantum eraser, whether interference or the complementary

which-path information is observed can be controlled by the experimenter's choice of the settings of polarizers placed

after the nal beam splitter of the interferometer. In the dispersion cancellation experiment, one cannot know, even

in principle, which of two photons propagated through a piece of the glass. This in turn leads to a cancellation

of the eect of dispersive broadening on the measurement. The fourth of these experiments shows that, even at

the one-particle level, there exist nonlocal eects in quantum mechanics: in tunnelling there exist superluminal time

delays of the tunnelling particle.

--Opt cit Pp 15

 

OPT CIT REFERENCES

[1] Einstein A, Podolsky B and Rosen N 1935 Phys. Rev. 47 777

[2] Franson J D 1989 Phys. Rev. Lett. 62 2205

[3] Kwiat P G, Steinberg A M and Chiao R Y 1993 Phys. Rev. A 47 R2472

[4] Kwiat P G, Steinberg A M and Chiao R Y 1992 Phys. Rev. A 45 7729

[5] Steinberg A M, Kwiat P G and Chiao R Y 1992 Phys. Rev. Lett. 68 2421

[6] Steinberg A M, Kwiat P G and Chiao R Y 1993 Phys. Rev. Lett. 71 708

[7] Steinberg A M and Chiao R Y 1994 Phys. Rev. Submitted (quant-ph/9501013) Sub-femtosecond determination of trans-

mission delay times for a dielectric mirror (photonic bandgap) as a function of angle of incidence

[8] Bohm D 1983 in Quantum Theory and Measurement ed J A Wheeler and W H Zurek (Princeton: Princeton) p 356

[9] Freedman S J and Clauser J F 1972 Phys. Rev. Lett. 28 938

[10] Clauser J F and Shimony A 1978 Rep. Prog. Phys. 41 1881

[11] Aspect A, Dalibard J and Roger G 1982 Phys. Rev. Lett. 49 1804

[12] Bell J S 1964 Physics 1 195

[13] Rarity J G and Tapster P R 1990 Phys. Rev. Lett. 64 2495

[14] Schr·odinger E 1983 in Quantum Theory and Measurement ed J A Wheeler and W H Zurek (Princeton: Princeton) p 152

[15] Chiao R Y, Kwiat P G and Steinberg A M 1991 Proceedings Workshop on Squeezed States and Uncertainty Relations ed

D Han, Y S Kim and W W Zachary (NASA Conference Publication 3135) p 61

[16] Brendel J, Mohler E and Martienssen W 1992 Europhys. Lett. 20 575

[17] Rarity J G and Tapster P R 1994 Phys. Rev. Lett. 73 1923

[18] Clauser J F, Horne M A, Shimony A and Holt R A 1969 Phys Rev. Lett. 23 880

[19] Kwiat P G 1993 Nonclassical Eects from Spontaneous Parametric Down-Conversion: Adventures in Quantun Wonderland

PhD thesis (U C Berkeley)

[20] Scully M O, Englert B -G and Walther H 1991 Nature 351 111

[21] Feynman R P, Leighton R B and Sands M 1965 The Feynman Lectures on Physics (Reading, MA: Addison-Wesley) III

3-5

[22] Stern A Aharonov Y and Imry Y 1990 Phys. Rev. A 41 3436

[23] Jordan T F 1993 Phys. Rev. A 48 2449

[24] Hong C K, Ou Z Y and Mandel L 1987 Phys. Rev. Lett. 59 2044

[25] Steinberg A M and Chiao R Y 1994 Phys. Rev. A 49 3283

[26] Shih Y H and Alley C O 1988 Phys. Rev. Lett. 61 2921

[27] Ou Z Y and Mandel L 1988 Phys. Rev. Lett. 61 50

[28] Wheeler J A 1983 in Quantum Theory and Measurement ed J A Wheeler and W H Zurek (Princeton: Princeton) p 182

[29] Kwiat P G, Steinberg A M and Chiao R Y 1994 Phys. Rev. A 49 61

[30] Brillouin L 1960 Wave Propagation and Group Velocity (New York: Academic Press)

[31] Chiao R Y 1993 Phys. Rev. A 48 R34

[32] Steinberg A M, Kwiat P G and Chiao R Y 1992 Phys. Rev. A 45 6659

[33] MacColl L A 1932 Phys. Rev. 40 621

[34] Wigner E P 1955 Phys. Rev. 98 145

[35] B· uttiker M and Landauer R 1982 Phys. Rev. Lett. 49 1739

[36] Hauge E H and St"vneng J A 1989 Rev. Mod. Phys. 61 917

[37] Landauer R and Martin T 1994 Rev. of Mod. Phys. 66 217

[38] Landauer R 1989 Nature 341 567

[39] Landauer R 1993 Nature 365 692

[40] St"vneng J A and Hauge E H 1993 Phys. World 6 23

[41] Enders A and Nimtz G 1993 J. Phys. I 3 1089

[42] Nimtz G, Enders A and Spieker 1994 J. Phys. I 4 565; Steinberg A M 1994 J. Phys. I 4 1813

[43] Ranfagni A,Fabeni P, Pazzi G P, and Mugnai D 1993 Phys. Rev. E 48 1453

[44] Spielmann Ch, Szip·ocs R, Stigl A and Krausz F 1994 Phys. Rev. Lett. 73 2308

[45] Yablonovitch E and Leung K M 1991 Physica 175B 81 and references therein

[46] B· uttiker M 1983 Phys. Rev. B 27 6178

[47] Jeers J and Barnett S M 1993 Phys. Rev. A 47 3291

[48] Aharonov Y and Vaidman L 1988 Phys. Rev. Lett. 58 1351

[49] Steinberg A M 1994 Phys. Rev. Lett. submitted (quant-ph/9501015) How much time does a tunnelling particle spend in

the barrier region?

[50] Steinberg A M 1994 Phys. Rev. A submitted Conditional probabilities in quantum theory, and the tunnelling time controversy

[51] Steinberg A M 1994 When Can Light Go Faster Than Light? The tunnelling time and its sub-femtosecond measurement

via quantum interference PhD thesis (U C Berkeley)

---

---

 

APPLY TO MONATOMIC INTERGEOMETRY AND MARCUS REID FREE ENERGY DEVICE OF 600% JOSEPHSON EFFECT, AS A VORTEXIJAH CONFIRMATION (600 % gained when he followed our advice in making improvements therein)

 

In 1962 Josephson predicted the existence of a tunnelling supercurrent which traversed a gap separating two superconductors. This superconducting tunnel effect was conrmed experimentally by Giaever and others in Josephson junctions consisting of superconducting thin lms separated by a thin oxide barrier.

----tunnelling Times and Superluminality: a Tutorial. Raymond Y. Chiao. Dept. of Physics, Univ. of California. Berkeley, CA 94720-7300, U. S. A. November 6, 1998

Does the click of the detector which registers the

arrival of the photon which traversed the tunnel barrier go o earl ier or later

(on the average) than the click of the detector which registers the arrival the

photon which traversed the vacuum? If the tunnel barrier had simply been a

thin piece of transparent glass, then the answer would obviously be \later,"

since the group velocity for a photon inside the glass would be less than the

speed of light, and the group delay for the photon traversing the glass relative

to that of the vacuum would be positive. However, if, as some tunnelling-time

theories predict, the tunnelling process is superluminal, then the counterintuitive answer would be \earlier," since the eective group velocity for a photon inside the tunnel barrier would be greater than the speed of light, and the group delay for the photon traversing the barrier relative to that of the vacuum would be negative. Hence it is the sign of the relative time between the clicks in the two

detectors which determines whether tunnelling is subluminal or superluminal.

The reader may ask why relativistic causality is not violated by the super-

luminality of the tunnelling process, if it should indeed be superluminal. It has

been shown [8] that special relativity does not forbid the group velocity to be

faster than c; only Sommerfeld's front velocity must not exceed c. Alsore-

member that due to the uncertainty principle the time of emission of the signal

photon is not under the experimenter's control.

Presently, the best detectors for photons have picosecond-scale response

times, which are still not fast enough to detect the femtosecond-scale time dif-

ferences expected in our tunnelling-time experiment. Hence it was necessary to

utilize a Hong-Ou-Mandel interferometer, which has a femtosecond-scale tem-

poral resolution for measuring the time dierence between the travel times of

the two photons traversing the two arms of the interferometer. By placing the

tunnel barrier in one of these arms, a precise measurement of the delay due to

tunnelling could then be performed.

The tunnel barrier used in our experiments was a dielectric mirror in which

periodic layers of alternately high and low index media produce a photonic

band gap at the rst Brillouin zone edge. The problem of photon propagation

in this periodic structure is analogous to that of the Kronig-Penney model for

electrons propagating inside a crystal. In particular, near the midgap point

on the rst Brillouin zone edge, there exists due to Bragg re ection inside the

periodic structure an evanescent (i.e., exponential) decay of the transmitted

wave amplitude, which is equivalent to tunnelling. Note that this Bragg re ection

eect is completely analogous to the one occurring in the Esaki tunnel diode

mentioned above. One important feature of this kind of tunnel barrier is the

fact that it is nondispersive near midgap, and therefore there is little distortion

of the tunnelling wave packet.

tunnelling Time Theories

Another strong motivation for performing experiments to measure the tunnelling

time was the fact that there were many con icting theories for this time (see

the reviews by Hauge and St"vneng [9], by Landauer and Martin [10], and by

Chiao and Steinberg [8]). It suces here to list the three main contenders:

(1) The Wigner time (i.e., \phase time" or \group delay").

(2) The B· uttiker-Landauer time (i.e., \semiclassical time").

(3) The Larmor time (with B· uttiker's modication).

The Wigner time calculates how long it takes for the peak of a wave packet

to emerge from the exit face of the tunnel barrier relative to the time the peak

of the incident wave packet arrives at the entrance face. Since the peak of the

wave packet in the Born interpretation is the point of highest probability for

a click to occur(seetheaboveGedankenexperiment), it is natural to expect

this to be the relevant time for our experiments. This calculation is based on

an asymptotic treatment of tunnelling as a scattering problem, and utilizes the

method of stationary phase to calculate the position of the peak of a wave

packet. The result is simple: this tunnelling time is the derivative of the phase

of the tunnelling amplitude with respect to the energy of the particle.

The B· uttiker-Landauer time is based on a dierent Gedankenexperiment.

Suppose that the height of the tunnel barrier is perturbed sinusoidally in time.

If the frequency of the perturbation is very low, the tunnelling particle will see

the instantaneous height of the barrier, and the transmission probability will

adiabatically follow the perturbation. However, as one increases the frequency

of the perturbation, at some characteristic frequency the tunnelling probability

will no longer be able to adiabatically follow the rapidly varying perturbation.

It is natural to dene the tunnelling time as the inverse of this characteristic

frequency. The result is again simple: for opaque barriers, this tunnelling time

is the distance traversed by the particle (i.e., the barrier width d) divided by

the absolute value of the velocity of the particle j v j . (In the classically forbidden

region of the barrier, this velocity is imaginary, but its characteristic size is given

by the absolute value).

The Larmor time is based on yet another Gedankenexperiment. Suppose that

the tunnelling particle had a spin magnetic moment (e.g., the electron). Suppose

further that a magnetic eld were applied to region of the barrier, but only to

that region. Then the angle of precession of the spin of the tunnelling particle

is a natural measure of the tunnelling time. However, B· uttiker noticed that in

addition to this Larmor precession eect, there is a considerable tendency for

the spin to align itself either along or against the direction of the magnetic eld

during tunnelling, since the energy for these two spin orientations is dierent.

The total angular change of the tunnelling particle's spin divided by the Larmor

precession frequency is B· uttiker's Larmor time.

One consequence of the Wigner time is the Hartman eect: The tunnelling

time saturates for opaque barriers, and approaches for large d a limiting value given by the uncertainty principle, h=(V0 E). The apparent superluminality

of tunnelling is a consequence of this eect, since as d is increased, there is a

point beyond which the saturated value of the tunnelling time is exceeded by

the vacuum traversal time d=c, and the particle appears to have tunneled faster

than light.

By contrast, the B· uttiker-Landauer theory predicts a tunnelling time which

increases linearly with d for opaque barriers, as one would expect classically.

For a rectangular barrier with a height V0 << mc 2 , the eective velocity j v j is

always less than c. However, for the periodic structure which we used in our

experiment, the effective velocity j v j at midgap is infinite, which is a behavior

even more superluminal than that predicted by the Wigner time. This fact

makes it easy to distinguish experimentally between these two theories of the

tunnelling time. However, we hasten to add that the B· uttiker-Landauer time

may not apply to our experimental situation, as the Gedankenexperiment on

which it is based is quite dierent from the one relevant to our experiment.

B·uttiker's Larmor time predicts a tunnelling time which is independent of d

for thin barriers, but which asymptotically approaches a linear dependence on d

in the opaque barrier limit, where it coincides with the B·uttiker-Landauer time.

In our rst experiment it was impossible to distinguish experimentally between

this time and the Wigner time. Only in our second experiment could these two

theories be clearly distinguished from one another.

 

Details of the Berkeley Experiments

Spontaneous parametric down-conversion was the light source used in our ex-

periments [11, 12]. An ultraviolet (UV) beam from an argon laser operating at

a wavelength of 351 nm was incident on a crystal of potassium dihydrogen phos-

phate (KDP), which has a " (2) nonlinearity. During the process of parametric

down-conversion inside the crystal, a rainbow of many colors was generated in

conical emissions around the ultraviolet laser beam, in which one parent UV

photon broke up into two daughter photons, conserving energy and momentum.

The KDP crystal was cut with an optic axis oriented so that the two degener-

ate (i.e., equal energy) daughter photons at a wavelength of 702 nm emerged

at a small angle relative to each other. We used two pinholes to select out

these two degenerate photons. The size of these pinholes determined the band-

width of the light which passed through them, and the resulting single-photon

wavepackets had temporal widths around 20 fs and a bandwidth of around 6

nm in wavelength.

The tunnel barrier consisted of a dielectric mirror with eleven quarter-

wavelength layers of alternately high index material (titanium oxide with n =

2:22) and low index material (fused silica with n = 1:45). The total thickness

of the eleven layers was 1.1 m. This implied an in vacuo traversal time across

the structure of 3.6 fs. Viewed as a photonic bandgap medium, this periodic structure had a lower band edge located at a wavelength of 800 nm and an upper band edge at 600 nm. The transmission coecient of the two photons which

were tuned near midgap (700 nm) was 1%. Since the transmission had a broad

minimum at midgap compared to the wave packet bandwidth, there was little

pulse distortion. The Wigner theory predicted at midgap a tunnelling delay time

of around 2 fs, or an effective tunnelling velocity of 1:8 c. The B·uttiker-Landauer

theory predicted at midgap an infinite eective tunnelling velocity, which implies

a zero tunnelling time.

To achieve the femtosecond-scale temporal resolutions necessary for measur-

ing the tiny time delays associated with tunnelling, we brought together these

two photons by means of two mirrors, so that they impinged simultaneously at

a beam splitter before they were detected in coincidence by two Geiger-mode

silicon avalanche photodiodes. There resulted a narrow null in the coincidence

count rate as a function of the relative delay between the two photons, a de-

structive interference effect first observed by Hong, Ou, and Mandel [13]. The

narrowness of this coincidence minimum, combined with a good signal-to-noise

ratio, allowed a measurement of the relative delay between the two photons to

a precision of 0:2 fs.

A simple way to understand this two-photon interference is to apply Feyn-

man's rules for the interference of indistinguishable processes. Consider two

photons impinging simultaneously on a 50/50 beam splitter followed by two de-

tectors in coincidence detection. When two simultaneous clicks occur at the two

detectors, it is impossible even in principle to tell whether both photons were re-

flected by the beam splitter or whether both photons were transmitted through

the beam splitter. In this case, Feynman's rules tell us to add the probability

amplitudes for these two indistinguishable process, and then take the absolute

square to find the probability. Thus the probability of a coincidence count to

occur is given by j r 2 + t 2j 2 , wherer is the complex reflection amplitude for one

photon to be reflected, and t is the complex transmission amplitude for one

photon to be transmitted. For a lossless beam splitter, time-reversal symmetry

leads to the relation t = ± ir. Substituting this into the expression for the coin-

cidence probability, and using the fact that j r j = j t j for a 50/50 beam splitter,

we find that this probability vanishes. Thus the two photons must always pair

off in the same (random) direction towards only one of the two detectors, an

effect which arises from the bosonic nature of the photons.

A schematic of the apparatus we used to measure the tunnelling time is given

in Fig. 2. The delay between the two daughter photons was adjustable by means

of the \trombone prism" mounted on a Burleigh inchworm system, and was

measured by means of a Heidenhein encoder with a 0.1 m resolution. A positive

sign of the delay due to a piece of glass was determined as corresponding to a

motion of the prism towards the glass. The multilayer coating of the dielectric

mirror (i.e., the tunnel barrier) was evaporated on only half of the glass mirror

substrate. This allowed us to translate the mirror so that the beam path passed

either through the tunnel barrier in an actual measurement of the tunnelling time, or through the uncoated half of the substrate in a control experiment. In

this way, one could obtain data with and without the barrier in the beam, i.e.,

a direct comparison between the delay through the tunnelling barrier and the

delay for traversing an equal distance in air. The normalized data obtained in

this fashion is shown in Fig. 3(a), with the barrier oriented at normal incidence

( = 0). Note that the coincidence minimum with the tunnel barrier in the

beam is shifted to a negative value of delay relative to that without the barrier in

the beam. This negative shift indicates that the tunnelling delay is superluminal.

To double-check the sign of this shift, which is crucial for the interpretation of

superluminality, we tilted the mirror towards Brewster's angle for the substrate

( = 56), where there is a very broad minimum in the re ection coecient as

a function of angle. Near Brewster's angle this minimum is so broad that it

is not very sensitive to the dierence between the high and low indices of the

successive layers of dielectrics. Thus to a good approximation, the re ections

from all layers vanish simultaneously near this angle. Hence the Bragg re ection

responsible for the band gap disappears, and the evanescent wave behavior and

the tunnelling behavior seen near normal incidence disappears. The dielectric

mirror should then behave like a thin piece of transparent glass with a positive

delay time relative to that of the vacuum. Detailed calculations not using the

above approximations also show that at = 55, the sign of the shift should

indeed revert to its normal positive value.

The data taken in p-polarization at = 55 is shown in Fig. 3(b). The

reversal of the sign of the shift is clearly seen. Therefore one is confronted witha choice of the data either in Fig. 3(a) as showing a superluminal

shift. Since we know that the delay in normal dielectrics as represented by

Fig. 3(b) should be subluminal, this implies that the tunnelling delay in Fig. 3(a) or in Fig. 3(b)

should be superluminal. Therefore the data in Fig. 3(a) implies that after

traversing the tunnel barrier, the peak of a photon wave packet arrived 1:47 0:21 fs earl ier than it would had it traversed only vacuum.

 

Mirror (normalized)

Another reason for tilting the mirror is that one can thereby distinguish

between the Wigner time and B·uttiker's Larmor time, as they dier consid-

erably in the region near the band edge, which occurs near Brewster's angle.

This can be seen in Fig. 4, where there is a considerable divergence as the

band edge is approached between the solid line representing the theoretical

prediction of the Wigner time, and the long-dashed line representing that of

B·uttiker's Larmor time. The data points in Fig. 4 seem to rule out B· uttiker's

Larmor time (although again we hasten to add that this theory may not apply

to our experiment). The agreement with Wigner's theory is better, but there

are discrepancies which are not understood.

Other experiments conrming the superluminality of tunnelling have been

performed in Cologne, Florence, and Vienna [14, 15, 16]. The Cologne and

Florence groups performed microwave experiments, and the Vienna group per-

formed a femtosecond laser experiment. All these groups have conrmed the

Hartman eect. One of these groups [17] has claimed to have sent Mozart's

40th symphony at a speed of 4:7c through a microwave tunnel barrier 114 mm

long consisting of a periodic dielectric structure similar to our dielectric mirror.

However, the further implication that their experiment represents a violation of

causality is in our opinion unfounded [8].

Recently, an experiment indicating the simultaneous existence of two different tunnelling times was performed in Rennes [18]. In frustrated total re ection

(FTIR), the tunnelling of photons through an air gap occurs between two glass

prisms when a light beam is incident upon this gap beyond the critical angle.

The Rennes group observed in FTIR both a lateral displacement of the tunnelling

beam of light and an angular de ection of this beam. These two eects could

be interpreted as evidence for two dierent tunnelling times that simultaneously

occurred in the same tunnelling barrier. The lateral displacement is related to

the Wigner time, and the angular de ection is related to the B· uttiker-Landauer

time. As evidence for this, they cited the saturation of the beam displacement

(the Hartman eect), and the linear increase of the beam de ection, as the gap

was increased.

 

Conclusions

The experiments at Berkeley and elsewhere thus indicate that the tunnelling pro-

cess is superluminal. In our opinion, this does not imply that one can communi-

cate faster than c, despite claims to the contrary by Heitmann and Nimtz [17].

The group velocity cannot be identied as the signal velocity of special relativ-

ity, by which a cause is connected to its eect. Rather, it is Sommerfeld's front

velocity which exclusively plays this role. However, even if one were to dene

the group velocity as a \signal" velocity, no causal loop paradoxes can arise [19].

Although the controversies amongst the various tunnelling theories have not

yet been fully resolved by experiment, a good beginning has been made in this direction.

In particular, it is now clear that one cannot rule out the Wigner

time simply on the grounds that it yields a superluminal tunnelling time. It

also appears that there may exist more than one tunnelling time. Hopefully,

the mysterious role of time in quantum mechanics will be elucidated by these

studies.

 

Acknowledgments

I would like to thank Prof. Rodolfo Bonifacio for inviting me to give the opening

lecture of this conference on the mysteries, puzzles, and paradoxes of quantum

physics. I would also like to thank Dr. Paul Kwiat and Prof. Aephraim Steinberg

for their collaboration on the Berkeley experiments, and for many helpful discus-

sions. This work was supported by the ONR under Grant No. N000149610034.

References

[1] F. Hund, Zeitschrift f· ur Physik 43 (1927) 805.

[2] L. Nordheim, Zeitschrift f· ur Physik 46 (1927) 833.

[3] J. R. Oppenheimer, Phys. Rev. 31 (1928) 66; Proc. Nat. Acad. Sci. 14

(1928) 363.

[4] G. Gamow, Zeitschrift f· ur Physik 51 (1928) 204; 52 (1928) 510.

[5] R. W. Gurney and E. U. Condon, Nature 122 (1928) 439; Phys. Rev. 33

(1929) 127.

[6] R. H. Fowler and L. Nordheim, Proc. Roy. Soc. (London) A119 (1928) 173.

[7] C. Zener, Proc. Roy. Soc. (London) 145 (1934) 523.

[8] R.Y. ChiaoandA. M. Steinberg, inProgress in Optics XXXVII, E. Wolf,

ed., (Elsevier, Amsterdam, 1997), p. 345.

[9] E. H. Hauge and J. A. St"vneng, Rev. Mod. Phys. 61 (1989) 917.

[10] R. Landauer and Th. Martin, Rev. Mod. Phys. 66 (1994) 217.

[11] A. M. Steinberg, P. G. Kwiat, and R. Y. Chiao, Phys. Rev. Lett. 71(1993)

708.

[12] A. M. Steinberg, and R. Y. Chiao, Phys. Rev. 51(1995) 3525.

[13] C. K. Hong, Z. Y. Ou and L. Mandel, Phys. Rev. Lett. 59 (1987) 2044.

[14] A. Enders and G. Nimtz, J. Phys. I France 3 (1993) 1089.

[15] A. Ranfagni, P. Fabeni, G.P. Pazzi and D. Mugnai, Phys. Rev. E 48(1993)

1453.

[16] Ch. Spielmann, R. Szip· ocs, A. Stingl and F. Krausz, Phys. Rev. Lett.

73(1994) 2308.

[17] W. Heitmann and G. Nimtz, Phys. Lett. A 196(1994) 154.

[18] Ph. Balcou and L. Dutriaux, Phys. Rev. Lett. 78(1997) 851.

[19] J. C. Garrison, M. W. Mitchell, R. Y. Chiao, and E. L. Bolda, Phys. Lett.

A 245 (1998) 19.

---

 

Other references of interest:

 

1.7 IS A LITTLE SHORT OF 1.618 ratio, if looked at figuratively. But it was Chiao's next experiments that yielded the 4.32 x C. I enclose these now for reference:

 

(3) Raymond Chiao (University of California at Berkeley, CA), and A. Y. Steinberg, Quantum

Optical Studies of tunnelling Times and Superluminality: Presents the experimental methods

and results of measuring the tunnelling time of a photon to cross a photonic band-gap tunnel

barrier, where an effective tunnelling speed of 1.7 times the speed of light is measured. The

author concludes, however, that information did not travel faster than light. (Chiao 1994)

 

Mozartz symphony number 40 is information.

Physics Approaching Speed of Light

Mind-bending new studies appear to break Einstein's rules

James Glanz, New York Times

Tuesday, May 30, 2000

The speed at which light travels through a

vacuum, about 186,000 miles per second, is

enshrined in physics lore as a universal speed

limit. Nothing can travel faster than that speed,

according to freshman textbooks and

conversation at sophisticated wine bars; if

anything could, Einstein's theory of relativity

would crumble, and theoretical physics would

fall into disarray.

Two new experiments have demonstrated how

flexible or misleading that comfortable wisdom

can be in the right circumstances. Using a

combination of atomic and electromagnetic

effects, researchers have produced light beams

in the laboratory that appear to travel much

faster than the normal speed of light. Einstein's

theory survives, physicists say, but the results

of the experiments, they agree, are

mind-bending.

In the most striking of the new experiments, a

pulse of light that passes through a transparent

chamber filled with specially prepared cesium

gas appears to be pushed to speeds of 300

times the normal speed of light. That is so fast

that, under these peculiar circumstances, the

main part of the pulse exits the chamber even

before it enters.

It is as if someone looking through a window at

home were to see a man slip and fall on a patch

of ice while crossing the street well before

witnesses on the sidewalk saw the mishap

occur -- a preview of the future. But Einstein's

theory, and at least a shred of common sense,

seem to survive, the physicists explain,

because the effect could never be used to

signal back in time to change the past and, in

the example, avert the accident.

A paper on the experiment, by Lijun Wang of

the NEC Research Institute in Princeton, N.J.,

has been submitted to the journal Nature and is

undergoing peer review. It is only the most

spectacular example of work by a wide range

of researchers who have recently produced

superluminal speeds of propagation in various

materials, in hopes of finding a chink in

Einstein's armor and of using the effect in

practical applications like speeding up

electrical circuits.

``It looks like a beautiful experiment,'' said

Raymond Chiao, a professor of physics at the

University of California at Berkeley, who, like a

number of physicists in the close-knit

community of optics research, is

knowledgeable about Wang's work.

LOOKING INTO THE FUTURE?

Chiao, whose own research laid some of the

groundwork for the experiment, added that

``there's been a lot of controversy'' over whether

the finding means that actual information -- like

the news of an impending accident -- could be

sent faster than c, the velocity of light. But he

said that he and most other physicists agreed

that it could not.

Though declining to provide details of his paper

because it is under review, Wang said: ``Our

light pulses can indeed be made to travel faster

than c. This is a special property of light itself,

which is different from a familiar object like a

brick,'' since light is a wave with no mass. A

brick could not travel so fast without creating

truly big problems for physics, not to mention

humanity as a whole.

INTERNATIONAL RESEARCH

A paper on the second new experiment, by

Daniela Mugnai, Anedio Ranfagni and Rocco

Ruggeri of the Italian National Research

Council, described what appeared to be slightly

faster-than-c propagation of microwaves

through ordinary air, and was published in the

May 22 issue of Physical Review Letters.

The kind of chamber in Wang's experiment is

normally used to amplify waves of laser light,

not speed them up, said Aephraim Steinberg, a

physicist at the University of Toronto. In the

usual arrangement, one beam of light is shone

on the chamber, exciting the cesium atoms,

and then a second beam passing through the

chamber soaks up some of that energy and gets

amplified when it passes through the atoms.

But the amplification occurs only if the second

beam is tuned to a certain precise wavelength,

Steinberg said. By cleverly choosing a slightly

different wavelength, Wang induced the cesium

to speed up a light pulse without distorting it in

any way. ``If you look at the total pulse that

comes out, it doesn't actually get amplified,''

Steinberg said.

Wang's experiment uses another property of

light signals. Light signals, consisting of

packets of waves, actually have two important

speeds: the speed of the individual peaks and

troughs of the light waves themselves, and the

speed of the pulse or packet into which they

are bunched.

WHEN LIGHT IS LIKE THE BAY

BRIDGE

A pulse may contain billions or trillions of tiny

peaks and troughs. In air the two speeds are

the same, but in the excited cesium they are

not only different, but the pulses and the waves

of which they are composed can travel in

opposite directions, like a pocket of congestion

on a highway, which can propagate back from a

toll booth as rush hour begins, even as all the

cars are still moving forward.

These so-called backward modes are not new

in themselves, having been routinely measured

in other media like plasmas, or ionized gases.

But in the cesium experiment, the outcome is

particularly strange because the backward light

waves can, according to the laws of quantum

mechanics, in effect, borrow energy from the

excited cesium atoms before giving it back a

short time later. The overall result is an

outgoing wave exactly the same in shape and

intensity as the incoming wave; the outgoing

wave just leaves early, before the peak of the

incoming wave even arrives.

©2000 San Francisco Chronicle

NOTES: 300 TIMES 186,000 = 55,800,000 = 34,487,021.01 X Phi, a very slight margin off, unfortunately this is a generally rounded off figure from 186,286. So it onn\ly remains interesting in the nautical miles universal measurement sense, which geometrically logs into everything of significance on this planet, and life.

Eureka! Scientists break speed of light

Jonathan Leake, Science Editor

Times Newspapers Ltd

June 4 2000

 

SCIENTISTS claim they have broken the ultimate speed barrier:

the speed of light.

In research carried out in the United States, particle physicists

have shown that light pulses can be accelerated to up to 300

times their normal velocity of 186,000 miles per second.

The implications, like the speed, are mind-boggling. On one

interpretation it means that light will arrive at its destination

almost before it has started its journey. In effect, it is leaping

forward in time.

Exact details of the findings remain confidential because they

have been submitted to Nature, the international scientific journal,

for review prior to possible publication.

The work was carried out by Dr Lijun Wang, of the NEC research

institute in Princeton, who transmitted a pulse of light towards a

chamber filled with specially treated caesium gas.

Before the pulse had fully entered the chamber it had gone right

through it and travelled a further 60ft across the laboratory. In

effect it existed in two places at once, a phenomenon that Wang

explains by saying it travelled 300 times faster than light.

The research is already causing controversy among physicists.

What bothers them is that if light could travel forward in time it

could carry information. This would breach one of the basic

principles in physics - causality, which says that a cause must

come before an effect. It would also shatter Einstein's theory of

relativity since it depends in part on the speed of light being

unbreachable.

This weekend Wang said he could not give details but confirmed:

"Our light pulses did indeed travel faster than the accepted speed

of light. I hope it will give us a much better understanding of the

nature of light and how it behaves."

 

Dr Raymond Chiao, professor of physics at the University of

California at Berkeley, who is familiar with Wang's work, said he

was impressedby the findings. "This is a fascinating experiment,"

he said.

In Italy, another group of physicists has also succeeded in

breaking the light speed barrier. In a newly published paper,

physicists at the Italian National Research Council described how

they propagated microwaves at 25% above normal light speed.

The group speculates that it could be possible to transmit

information faster than light

 

[I will be looking more into this particular finding, which sounds outstanding, with microwaves, denucleated DNA ATP-ADP microwaves and Pinoline harmonic overtone cancellation of its Electron Spin Resonance whilst bonding with Adenine in the denucleated DNA, and loosing its electrical resistence (superconducting, by sonic ESR wave cancellation, as iterated in The Unity Keys Of Emmanuel), and transmitting the entire DNA sonic matrix complexity, as well as the virtual, with the Microwave component now enabled into post c propagation, the implications are even more astounding in terms of the Diamond Body et al. -Ananda].

 

Dr Guenter Nimtz, of Cologne University, an expert in the field,

agrees. He believes that information can be sent faster than light

and last week gave a paper describing how it could be done to a

conference in Edinburgh. He believes, however, that this will not

breach the principle of causality because the time taken to

interpret the signal would fritter away all the savings.

"The most likely application for this is not in time travel but in

speeding up the way signals move through computer circuits," he

said.

Wang's experiment is the latest and possibly the most important

evidence that the physical world may not operate according to

any of the accepted conventions.

In the new world that modern science is beginning to perceive,

sub-atomic particles can apparently exist in two places at the

same time - making no distinction between space and time.

Separate experiments carried out by Chiao illustrate this. He

showed that in certain circumstances photons - the particles of

which light is made - could apparently jump between two points

separated by a barrier in what appears to be zero time. The

process, known as tunnelling, has been used to make some of the

most sensitive electron microscopes.

The implications of Wang's experiments will arouse fierce debate.

Many will question whether his work can be interpreted as proving

that light can exceed its normal speed - suggesting that another

mechanism may be at work.

Neil Turok, professor of mathematical physics at Cambridge

University, said he awaited the details with interest, but added: "I

doubt this will change our view of the fundamental laws of

physics."

Wang emphasises that his experiments are relevant only to light

and may not apply to other physical entities. But scientists are

beginning to accept that man may eventually exploit some of

these characteristics for inter-stellar space travel.

 

Copyright 2000 Times Newspapers Ltd. This service is provided on

Times Newspapers' standard terms and conditions. To inquire about a

licence to reproduce material from The Sunday Times, visit the

Syndication website.

The Scientific American, September 2000 issue, entitled "Unlimited Light", pp 18, reiterating what was published in Nature, July 20, by Dr. Wang, gives some interesting angles on some of these experiments in terms of coherency of waves, to say the least, I quote (my emphasis):

 

"The researchers used a combination of laser beams to create an usual region of 'anomolous dispersion' in the six centimeters of cesium gas, where the velocity of light is higher for higher frequencies of light (ordinarily higher frequencies mean lower speeds).

"This region causes the pulse to 're-phase,' according to Wang. The light pulse, all of whose constituent wavelengths overlap constructively, loses its phase alignment as it propagates toward the cell, causing the waves to cancel one another out. Inside the cell, anomalous dispersion causes shorter wavelength components of the pulse to become longer, and vice versa. That enables the waves to attain phase alignment after exciting the cell. The result is the same pulse but advanced in time by a factor of 310 -- specifically, 62 nanoseconds better than the 0.2 nanosecond it takes for light to travel that distance in a vacuum.

"Some physicists, such as Raymond Chiao of the University of California at Berkley, have viewed the effect as pulse reshaping akin to squeesing a long baloon filled with water. The cesium atoms amplify the early, front parts of the pulse by stimulated emission of radiation (the qunatuim process that creates laser beams), whereas later parts are deamplified by stimulated absorption. In other words, the system re-creates the entire pulse based on the front part of the pulse, 'Nature knows how to extrapolate from the information that you gave in the ealier parts of the pulse,' explains Chiao, who with his Berkeley colleague Morgan Mitchell constructed a simple band-pass amplifier that also exhibited a negative group delay, advancing a 25-millisecond pulse by several milliseconds."

All new Pictorial Summary: ../summary (link at sitemap)